砲弾の大型化のデメリット
もっとも、遠距離でも貫通力を増大させる最良の方法は、砲の口径を大きくし(大口径の弾を使用するということ)、かつ、砲身長を長くすることだ。しかし大口径の長い砲を戦車に搭載するということはそれだけ重量増加を招き、戦車の特徴の一つである機動性を失わせることになる。
また、大口径の砲を使用することは、砲弾の大型化と重量増につながる。大口径かつ大型の弾体を発射して飛行させ、それなりの貫通力を持たせるためには発射に必要な炸薬の量もそれだけ増やさなければならないからである。
そうなると、砲弾が大型で重くなっていき、戦車の装填手が1人では持て余すほどになって、弾体と薬莢を別々にした薬のう式砲弾を使用しなければならなくなった(自動装填装置があれば別だが、120ミリ砲が主流となっている現在でも、自動装填装置を装備した戦車はごく一部にすぎない。当然、第二次世界大戦当時には開発されていなかった)。
さらに、砲弾の大型化と重量増は、戦車に搭載できる砲弾の数をも減少させることになる。ソ連軍のIS2戦車は大口径の122ミリ砲を装備したが、搭載できる砲弾はわずか28発しかなかった。

戦車砲の大口径化は貫通力の増大をもたらしたが、その反面、戦車にかかる反動も非常に大きなものとなった。重量についても同様のことがいえる。
砲の重量増加はそれを載せるための車体強度(装甲の強度ではなく、重い砲や砲塔を載せて未整備の道路や原野などを充分に走行できるための操向装置や車体の強度)も向上させねばならない。その結果、戦車の重量自体が増加し、機動性を失わせてしまう。
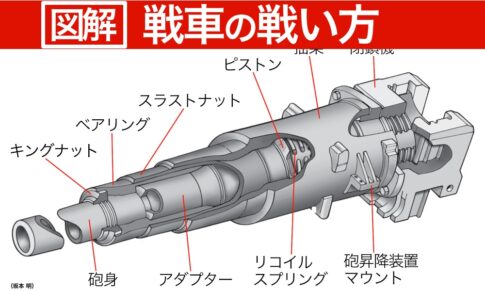
このため、反動を小さくする方法として砲口制退器(マズル・ブレーキ)が取り付けられることがある。この装置は弾体が砲身を出るときに、砲身の中の高圧ガスを砲口部に左右(あるいは上下)に穴けた開口部から逃がして、駐退復座機にかかる反動を弱めるためのものだ。
しかし、これには吹き出したガスが横に広がるため、弾着を見ることができないという欠点もある。












コメントを残す